
2차원 그리드 포인트 생성
지난 시간에 대한 추가부분입니다.
변수가 2개인 2차원 함수를 그래프를 그리거나, 표를 작성할 때 사용하는
2개의 좌표값 쌍을 그리드 포인트라고 합니다.
(x,y) = (0,0), (0,1), (0,3), (0,4), (1,0), (2,0) .... (2,4)
numpy의 meshgrid는 사각형 영역을 구성하는 가로축의 점들과
세로축의 점들을 나타내는 두 벡터를 인수로 받아서
사각형 영역을 이루는 조합을 출력 합니다.
x = np.arange(3)
y = np.arange(5)
x,y(array([0, 1, 2]), array([0, 1, 2, 3, 4]))
X, Y = np.meshgrid(x,y)
Xarray([[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2]])
Yarray([[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3],
[4, 4, 4]])
x, y를 인수로 받아서 한줄씩 리스트로 만드는
함수 생성
for x, y in zip(X,Y):
print(list(zip(x,y)))[(0, 0), (1, 0), (2, 0)]
[(0, 1), (1, 1), (2, 1)]
[(0, 2), (1, 2), (2, 2)]
[(0, 3), (1, 3), (2, 3)]
[(0, 4), (1, 4), (2, 4)]
2차원 배열로 확인
[list(zip(x, y)) for x, y in zip(X, Y)][[(0, 0), (1, 0), (2, 0)],
[(0, 1), (1, 1), (2, 1)],
[(0, 2), (1, 2), (2, 2)],
[(0, 3), (1, 3), (2, 3)],
[(0, 4), (1, 4), (2, 4)]]
기존보다 시각화가 되어 표시되었습니다
서론
벡터화 연산은 numpy의 두번째 시간에도 확인해본적이
있습니다. 하지만 다시 나왔죠?🥂
브로드캐스팅이라는 새로운 기능이 등장하면서
확장하는 계산 방법이 등장합니다.
연산은 머리가 아파지는 개념이지만😨
그만큼 중요하게 짚고 넘어가야 하는 내용이므로
한번 더 들어가보도록 하겠습니다😘
1. 벡터화 연산
우리는 명시적으로 반복문을 쓰지 않아도
배열의 모든 원소에 대해 반복 연산을 할 수 있습니다.
자, 선형대수에서 두 벡터의 합계를 보겠습니다.
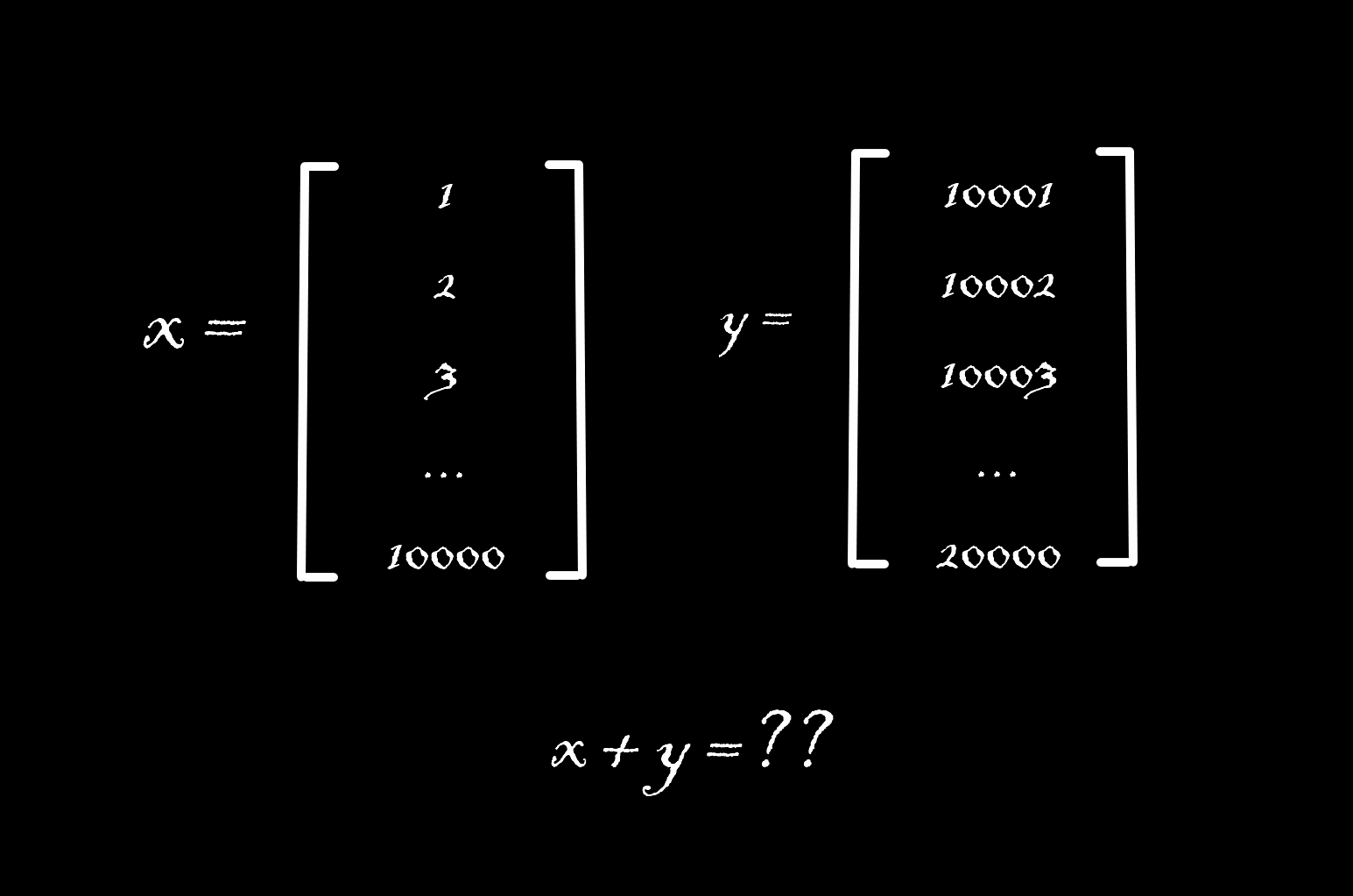

z = x + y로 설정하겠습니다.
배열의 형태로 모습만 약간 바뀌는 것 빼고는 연산 과정은
똑같습니다.
x = np.arange(1,10001)
y = np.arange(10001,20001)
x,y(array([ 1, 2, 3, ..., 9998, 9999, 10000]),
array([10001, 10002, 10003, ..., 19998, 19999, 20000]))
벡터화 연산을 사용하는 이유는 무엇일까요?
사용하지 않을 경우 이렇게 for문을 사용해야 합니다.
[0, 0, 0 .... 0] 으로 이루어진 행렬 z
z = np.zeros_like(x)
zarray([0, 0, 0, ..., 0, 0, 0])
for문으로 할당
for i in range(len(z)):
z[i] = x[i] + y[i]
zarray([10002, 10004, 10006, ..., 29996, 29998, 30000])
사칙 연산뿐만 아니라 비교연산 ↔ 논리연산도
벡터화 연산으로 가능합니다
a = np.array([0,1,2,3,4])
b = np.array([4,2,2,5,4])
a,b(array([0, 1, 2, 3, 4]), array([4, 2, 2, 5, 4]))
a와 b를 비교
a==barray([False, False, True, False, True])
a != barray([ True, True, False, True, False])
a >= barray([False, False, True, False, True])
좋습니다!
배열 원소를 일일히 비교하지 않고 모두 맞는지 비교하려면
np.all 함수를 사용하면 됩니다.
c = np.array([0,1,2,3,4])
a,b,c(array([0, 1, 2, 3, 4]), array([4, 2, 2, 5, 4]), array([0, 1, 2, 3, 4]))
np.all(a==c)True
배열의 원소 중 하나라도 이 조건을 만족시키는지
보려면 np.any를 사용합니다.
np.any(a==b)True
여러가지 수학에서의 함수도 벡터화 연산을 지원 합니다.
지수함수 exp ( ) 와 로그함수 log ( ) 입니다
a= np.arange(5)
aarray([0, 1, 2, 3, 4])
np.exp(a)array([ 1. , 2.71828183, 7.3890561 , 20.08553692, 54.59815003])
10 ** aarray([ 1, 10, 100, 1000, 10000])
np.log(a+1)array([0. , 0.69314718, 1.09861229, 1.38629436, 1.60943791])
2. 브로드캐스팅
벡터 즉 배열끼리 덧셈과 뺄셈같은 연산을 하려면
두 배열끼리의 크기가 일치해야 합니다. (행렬도 동일합니다)
numpy에서는 서로 다른 크기를 가진 두 배열의 사칙연산을
지원하는데요, 이를 브로드캐스팅(broadcasting)이라 합니다.
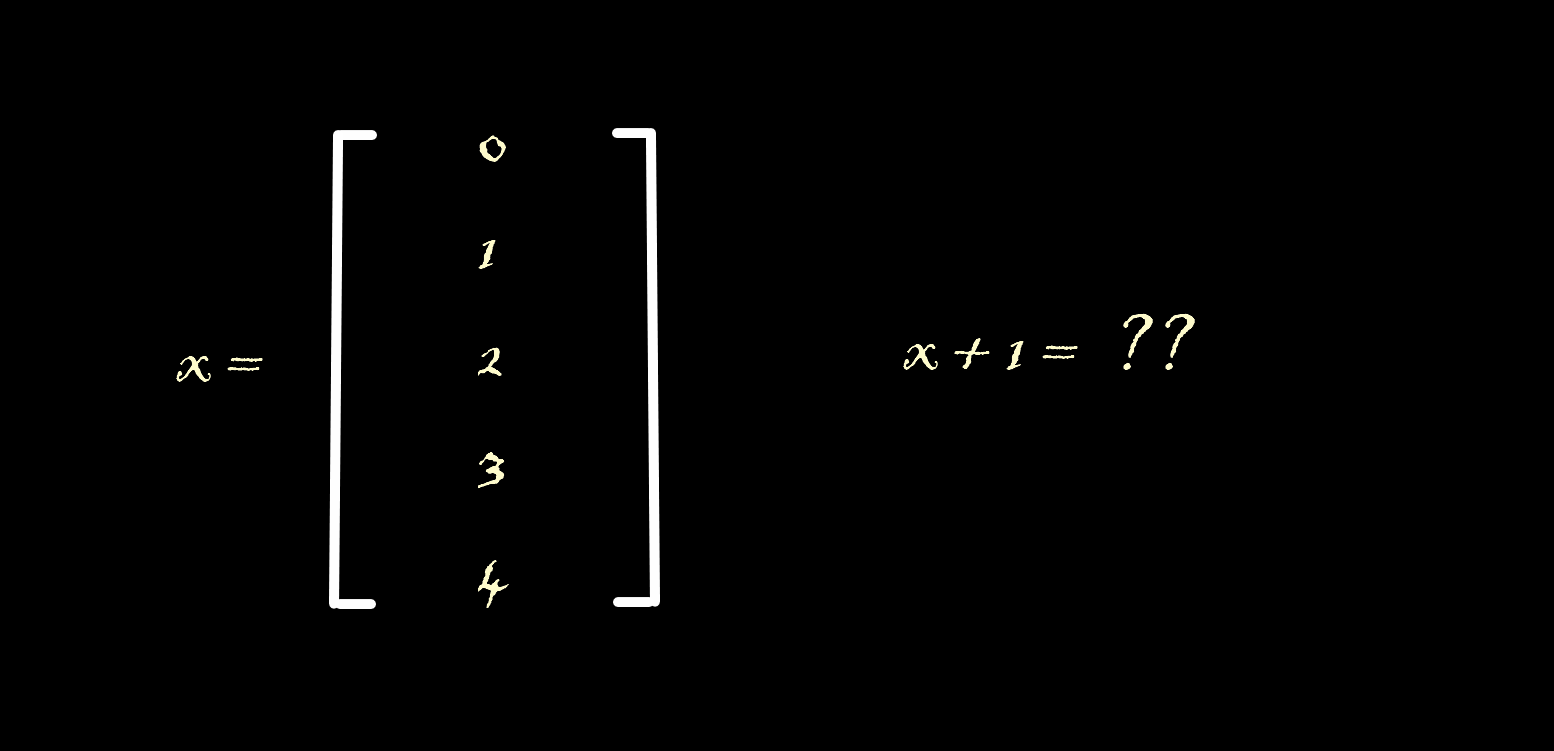

numpy에서 보겠습니다.
x+yx = np.arange(5)
y = np.ones_like(x)
x,y(array([0, 1, 2, 3, 4]), array([1, 1, 1, 1, 1]))
x+1array([1, 2, 3, 4, 5])
x+yarray([1, 2, 3, 4, 5])
2차원 배열 이상도 브로드캐스팅 됩니다.
x = np.vstack([range(7)[i:i+3] for i in range(5)])
x.shape(5, 3)
xarray([[0, 1, 2],
[1, 2, 3],
[2, 3, 4],
[3, 4, 5],
[4, 5, 6]])
y는 축을 늘리는 newaxis를 사용해보겠습니다.
y = np.arange(5)[:, np.newaxis]
y,y.shape(array([[0],
[1],
[2],
[3],
[4]]), (5, 1))
x와 y의 합을 나타냅니다.
x + yarray([[ 0, 1, 2],
[ 2, 3, 4],
[ 4, 5, 6],
[ 6, 7, 8],
[ 8, 9, 10]])
3. 차원 축소 연산
차원 축소라니, 이름만 들어도 멋있네요😎
행렬 하나의 행에 있는 원소들을 하나의 데이터 집합으로 보고
각 행에 처리된 연산으로 한 차원 낮은 벡터를 구성하게 하는
연산입니다.
특별히 난해한 점은 없을 겁니다
바로 들어가보겠습니다!
sum
합계입니다.
x = np.arange(1,5)
xarray([1, 2, 3, 4])
np.sum(x), x.sum()(10, 10)용법은 헷갈리지만 않으면 됩니다. x.sum을 써도 무방해요.
각 array의 값들을 더합니다.
min, max
최솟값과 최댓값을 뽑아줍니다.
x.min(), x.max()(1, 4)
np. 사용
np.min(x), np.max(x)(1, 4)
최솟값과 최댓값이 배열에서 서있는
위치도 알려줍니다.
x.argmin(), x.argmax()(0, 3)
mean,median
mean은 평균, median은 중간값을 의미합니다.
x = np.array([1,2,3,4,5,1])
np.mean(x)2.6666666666666665
np.median(x)2.5
불리언 연산 any, all
all은 모두가 True일 경우에만 True를 반환하며
any는 어떤 것 하나라도 True일 경우 True를 반환합니다.
np.all([True, True, False])False
np.any([True, False, False])True
2차원 이상에서의 차원 축소 연산은 어떻게 할까요?
바로, axis 인수를 사용해서 지시합니다.
axis = 0 인 경우에는 열 연산,
axis = 1 인 경우에는 행 연산,
default는 axis = 0입니다.
axis인수는 대부분의 차원 축소 명령에 적용할 수 있습니다
x = np.array([[1,2],[2,2],[3,4]])
xarray([[1, 2],
[2, 2],
[3, 4]])
axis없이는 모두 더해버립니다.
x.sum()14
axis를 지정하면 1행, 2행, 3행을 더합니다.
x.sum(axis=0)array([6, 8])
1열과 2열을 더합니다.
x.sum(axis=1)array([3, 4, 7])좋습니다.
이렇게 해서 간단하게
numpy 배열의 벡터화 연산을 알아보았습니다.
다음에는 정렬과 기술통계에 대해서 보겠습니다.
'Programming Language > Python_library' 카테고리의 다른 글
| 파이썬_응용단계 ep.8 난수와 샘플링, 데이터 카운팅! (2) | 2022.12.13 |
|---|---|
| 파이썬_응용단계 ep.7 정렬과 통계 (0) | 2022.12.11 |
| 파이썬_응용단계 ep.5 배열의 연결과 분할 (2) | 2022.12.09 |
| 파이썬_응용단계 ep.4 생성과 변형, 전치 (2) | 2022.12.08 |
| 파이썬_응용단계 ep.3 배열 깎는 조각가 (0) | 2022.12.08 |



