[Machine Learning] PCA + Dimension 축소 학습

서론

 

이전까지 머신러닝의 모델에서는 어느정도 column들이 정제된, 즉 피쳐가 보기좋게

들어가있는 모델들을 확인해보았습니다. 

 

하지만 현실에서 마주하는 여러가지 상황에서, 우리는 column들이 항상 잘 정제되어 있는

데이터만을 보긴 어렵습니다. 종종 변수가 연관관계를 지닐지, 지니지 않을지 정말

구분하기도 어려운 데이터프레임을 볼 때도 있습니다.

 

이러한 상황에서, 우리는 규칙성이 없던 것에 규칙성을 만들어보려고 하는

여러가지 시도들을 해보게 됩니다.

 

그러한 시도들 중의 하나가 바로 PCA 입니다.

 

---

Principal Component Analysis

 

본 글은 공돌이의 수학정리노트 에서 영감을 받았습니다.

▼링크
https://angeloyeo.github.io/2019/07/27/PCA.html

 

주성분 분석(PCA) - 공돌이의 수학정리노트

 

차원축소는 심리학의 조사와 연구를 진행하던 중 그 필요성이 두각되었다고 합니다.

 

일반적으로 심리학과의 몇가지 실험들에서는 자연에서 볼 수 있는 꽤 엄격하고

냉정한 값이 아닌 변칙적이고 예측에서 벗어나는 항목들을 자주 조사해오곤 했습니다.

 

선거를 예시로 들었을 때, 우리는 특정한 지역에서 일정한 범위에 드는 사람들이

투표한 대상을 확실히 추려낼 수 있습니다.

 

A시의 시장은 60%의 표를 얻었다, B시의 시장은 10%의 표를 얻었다.

 

이러한 결과는 가능합니다.

 

A시의 시장은 60%의 표를 얻었긴 한데
간혹 화가 나면 50%로 표가 감소하기도 한다.

 

이런 조사결과는 없겠죠?

 

 

헌데, 투표하는 사람의 마음도 어디 그런가요?

누군가를 뽑는 사람들의 마음은 밖으로 드러나지 않습니다. 

 

즉, 심리학에서의 연구대상은 겉으로 보이지 않습니다.

 

추상적이고 측정하기 모호한 것들을 어떻게 측정할 것인가

이에 대한 문제의식을 보는 것이 비지도 학습 입니다.

 

 

 

그중에서도 데이터들의 분산이 최대한 보존될 수 있도록 찾는 축을

principal component로, 한글로 주 성분 이라고 합니다.

 

이렇게 변수가 갖고 있는 축을 낮춰 더 낮은 차원으로 투영하는 것

이를 PCA의 원리라고 할 수 있습니다.

 

아래 그림을 한번 봐보겠습니다.

 

점 하나하나가 변수라고 생각한다면, 정말 수천에서 수만가지의 

컬럼들을 갖고 있다고 봐야할 것입니다. 언뜻 보기에도 점이나 선이라기 보다는

면으로 보입니다.

 

 

마치 철가루가 흩날리는 것 같군요.

이를 자석으로 모아보겠습니다.

 

 

 

 

 

(왼쪽 그림)이를 분산이 최대로 보존될 수 있는 값들을 찾아야 합니다.

 

여기에 자석처럼 분산을 최대로 보존할 수 있는 가장 Principal한 

축을 찾아서 직교하는 y값들을 찾아서 사영하면, 일종의 직선이 남을 수 있겠죠?

 

2차원이 1차원으로 변한 것입니다.

 

이렇게 PCA가 필요할 정도로 많은 feature를 보유한 데이터셋을

축소할 때 생기는 엄청난 시간을 획기적으로 단축할 수 있습니다.

 

 

이 방안은 주로 전체 분석과정 중, 초기에 데이터가 어떻게 생겼는지 파악할 때 사용합니다.

물론 직접 봐서 변수가 심각하게 많지 않은한 필수적인 단계는 아닙니다.

 

 

이번에는 실제 데이터셋을 통해서 차원을 축소하는 형태를 보겠습니다.

 

---

데이터 로드

 

필자는 임의의 데이터를 불러왔습니다. (해외 category별 카드 결제율)

 

각 value들은 거의 의미가 없는 상수들의 집합이니 무시하셔도 됩니다.

이렇게 13개 열을 갖고 있는 데이터입니다.

각 category는 결제한 곳을 엔터테인먼트, 외식, 식료품, 주유소, 건강 등의 군별로 범주화한 것입니다.

 

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 100 entries, 0 to 99
Data columns (total 13 columns):
 #   Column                   Non-Null Count  Dtype  
---  ------                   --------------  -----  
 0   amt                      100 non-null    float64
 1   category_entertainment   100 non-null    float64
 2   category_food_dining     100 non-null    float64
 3   category_gas_transport   100 non-null    float64
 4   category_grocery         100 non-null    float64
 5   category_health_fitness  100 non-null    float64
 6   category_home            100 non-null    float64
 7   category_kids_pets       100 non-null    float64
 8   category_misc            100 non-null    float64
 9   category_personal_care   100 non-null    float64
 10  category_shopping        100 non-null    float64
 11  category_travel          100 non-null    float64
 12  label                    100 non-null    int64  
dtypes: float64(12), int64(1)
memory usage: 10.3 KB

 

실제로 데이터 구조가 복잡해서, x와y축으로 하는 2차원 그래프로

나타내는 것은 어렵습니다.

 

지도학습때와 같이, X와 y를 구분합니다.

 

# 종속변수와 독립변수 분리 (X, y)
X = df.drop('label', axis=1) # 독립변수들
y = df.label # 종속변수

 

종속변수 확인합니다. 데이터셋에 함께 있었던 label입니다.

 

y

0     0
1     3
2     1
3     0
4     3
     ..
95    3
96    0
97    0
98    0
99    3
Name: label, Length: 100, dtype: int64

 

PCA를 사용하기 위해서, 사이킷런에 있는 새로운 패키지를 활용합니다.

바로 decomposition입니다. 번역하면 '분해'입니다.

 

# PCA 알고리즘
from sklearn.decomposition import PCA

수많은 변수들의 특성을 2개 정도로 합쳐서 처리해보겠습니다.

주성분 갯수를 2개로 선언합니다.

 

pca = PCA(n_components=2) 
# 주성분 갯수를 2로 지정 (여러 개의 변수들의 특성을 2개로 합쳐서 처리)

 

이제 독립변수를 학습시켜줍니다.

 

pca.fit(X)
df_pca = pca.transform(X) # 차원 축소 적용

 

PCA한 데이터프레임을 확인하면 어떻게 될까요.

PC를 2개 갖는 2차원 배열이 됩니다.

 

df_pca

분량 문제로 전체 데이터 중략

 

간단하게 시각화까지 진행해서 눈으로 드러내보겠습니다.

 

축을 기준으로 데이터프레임을 만들어봅니다.

 

df2 = pd.DataFrame(df_pca, columns = ['PC1', 'PC2'])
df2

 

아까 확인했던 종속변수를 join을 이용하여 결합해봅니다.

 

df2 = df2.join(y)
df2

 

산점도로 찍어보겠습니다. 색깔별 범례는 label입니다.

legend는 false로 해서 그래프상에서는 안보입니다.

 

plt.figure(figsize=(12,9))
sns.scatterplot(x = 'PC1', y ='PC2', hue = 'label', legend = False, data=df2, palette = 'rainbow')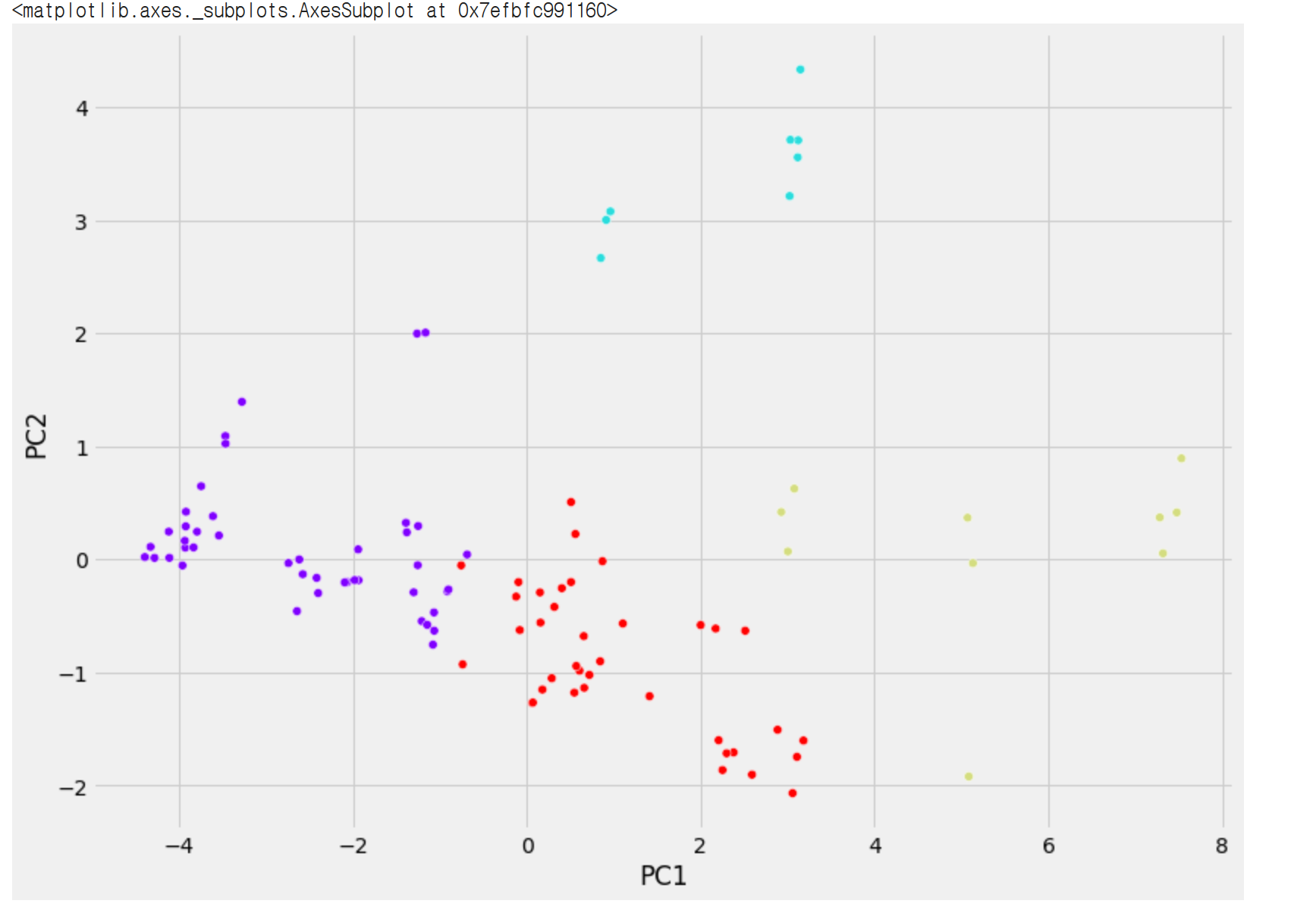

 

PC1, PC2를 기준으로 변수들이 나눠진 형태입니다.

이를 기존의 독립변수들과의 관계로 나타내면 다음과 같습니다.

 

pca.components_ # 각 주성분 pc1, pc2와 기존 독립변수 간의 관계 확인

array([[ 0.3484681 ,  0.32447242,  0.30303652,  0.14186907,  0.30618347,
         0.31297263,  0.29718852,  0.3045823 ,  0.29341337,  0.30287672,
         0.32053447,  0.08927503],
       [ 0.05827591,  0.06034266,  0.15264674, -0.54435586,  0.03109502,
         0.03790586,  0.23809571, -0.2315275 , -0.2471928 , -0.20898284,
         0.14479001,  0.65946781]])

 

기존의 X열들을 컬럼으로 하여 데이터프레임을 생성한 사례

 

df3 = pd.DataFrame(pca.components_, columns=X.columns, index = ['PC1','PC2'])
df3

amt	category_entertainment	category_food_dining	category_gas_transport	category_grocery	category_health_fitness	category_home	category_kids_pets	category_misc	category_personal_care	category_shopping	category_travel
PC1	0.348468	0.324472	0.303037	0.141869	0.306183	0.312973	0.297189	0.304582	0.293413	0.302877	0.320534	0.089275
PC2	0.058276	0.060343	0.152647	-0.544356	0.031095	0.037906	0.238096	-0.231528	-0.247193	-0.208983	0.144790	0.659468

 

위 데이터프레임을 heatmap으로 표현하여 시각화해봅니다.

글씨가 다 읽힐 수 있도록 xticks와 yticks의 각도를 따로 설정해줍니다.

 

plt.figure(figsize=(20,3))
sns.heatmap(df3, annot=True) # heatmap
plt.xticks(rotation=-15)
plt.yticks(rotation=0)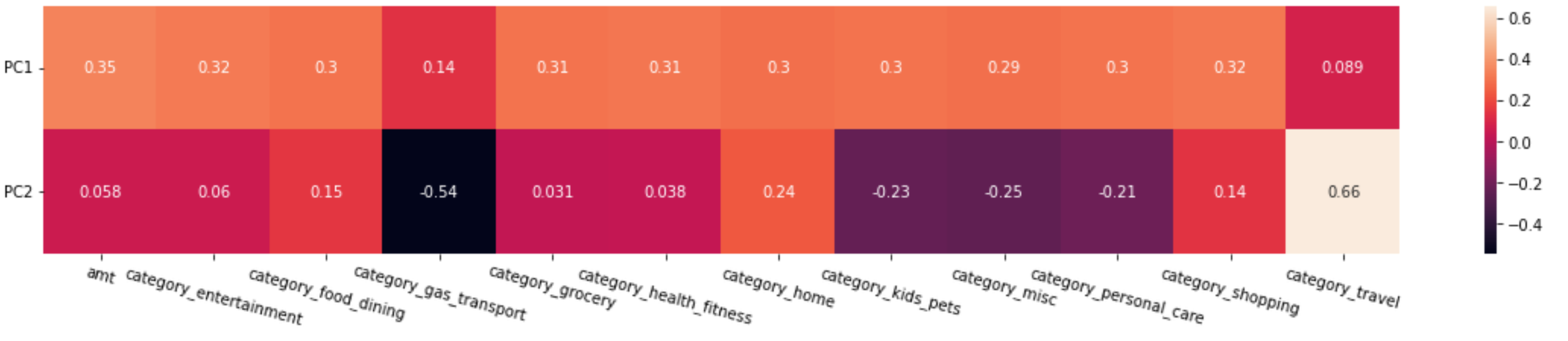

참조 : 주성분분석을 하기 전의 데이터프레임 표현

 

확연한 차이가 보이시나요?

---

여기까지 정리해서, PCA 정리와 실습 사례를 마치겠습니다.