
선형회귀란?
우리의 일상에서는 많은 지표와 숫자들이 있습니다.
지표와 숫자, 개체와 갯수, 데이터와 데이터 등의 관계에서
관계를 찾을 수도 있는데요.
이것이 저것을 불러오고, 어떤 것이 저런 것을 가져오는,
일종의 인과관계 를 상상할 수도 있습니다.
선형회귀는 여러가지 데이터들을 활용하여 연속형 변수인
목표 변수를 예측하는 것이 목적입니다.
즉, 연속된 변수를 우리가 예측하는 최적의 직선
그것을 찾는 알고리즘이 바로
선형 회귀 (Linear Regression) 입니다.
선형 회귀는 머신러닝의 기초적인 알고리즘 입니다.
복잡한 알고리즘에 비해 예측력이 떨어지지만 데이터의 특성이 복잡하지 않을 땐
더 쉽고 빠른 예측이 가능하기 때문에 자주 사용됩니다.
선형 회귀는 다른 모델과의 성능을 비교하는 기준 모델로 사용하기도 합니다.
이러한 방법의 장점과 단점은 무엇일까요?
장점은 모델이 간단하여 구현과 해석이 쉽다는 점입니다.
또한 모델링 소요 시간이 짧습니다.
단점은 최신 알고리즘에 비해 낮은 예측력을 갖는다는 점 인데요.
독립변수와 예측변수의 선형관계를 전제하기 때문에
이같은 전제에서 벗어나는 데이터에서는 예측력이 떨어질 수 있습니다.
즉, 상관관계에서 인과관계를 추론하는데, 이는 성급한 추론으로
이어질 수도 있는 것이죠.
선형회귀를 직접 진행해보겠습니다.
임포트
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib as plt
필자가 가져온 것은 데이터 자료 중, 캐글의 insuarance 데이터에서
추출한 지역, 성별, 흡연여부에 따른 보험비용(expenses) 액수 입니다.
df = pd.read_csv('https://raw.githubusercontent.com/bigdata-young/ai_26th/main/data/insurance.csv')
df
데이터 전처리
데이터를 모델링할 수 있게 다듬는 과정입니다.
이 데이터값들은 숫자여야 합니다.
df.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1338 entries, 0 to 1337
Data columns (total 7 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 age 1338 non-null int64
1 sex 1338 non-null object
2 bmi 1338 non-null float64
3 children 1338 non-null int64
4 smoker 1338 non-null object
5 region 1338 non-null object
6 expenses 1338 non-null float64
dtypes: float64(2), int64(2), object(3)
memory usage: 73.3+ KB저런, object가 3개나 있군요.
범주형 데이터 처리
smoker를 int로
df.smoker # smoker를 int로0 yes
1 no
2 no
3 no
4 no
...
1333 no
1334 no
1335 no
1336 no
1337 yes
Name: smoker, Length: 1338, dtype: object
df.smoker.eq('yes')0 True
1 False
2 False
3 False
4 False
...
1333 False
1334 False
1335 False
1336 False
1337 True
Name: smoker, Length: 1338, dtype: bool
yes는 1, no는 0으로 하고 싶어해요.
mul(1)은 1을 곱합니다.
df.smoker.eq('yes').mul(1) # (df.smoker == 'yes') * 10 1
1 0
2 0
3 0
4 0
..
1333 0
1334 0
1335 0
1336 0
1337 1
Name: smoker, Length: 1338, dtype: int64
자 smoker를 바꿔줍니다.
df.smoker = df.smoker.eq('yes').mul(1)
df.info()Data columns (total 7 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 age 1338 non-null int64
1 sex 1338 non-null object
2 bmi 1338 non-null float64
3 children 1338 non-null int64
4 smoker 1338 non-null int64
5 region 1338 non-null object
6 expenses 1338 non-null float64
dtypes: float64(2), int64(3), object(2)
memory usage: 73.3+ KB
object(2)가 되었습니다.
범주형 데이터 처리 > 더미 변수 (one-hot encoding)
두 개의 변수가 남았습니다.
sex = is male? is female?도 처리해야 하구요.
region = is northeast? is northeast? is southeast? is southwest? 이것도 처리해야 합니다.
(0,1)
(0,1,0,1)
등등
이럴땐 dummies (더미 변수 생성)을 통해서 진행할 수 있습니다.
# pd.get_dummies(df, columns=[내가 변환시키고 싶은 컬럼 이름들])
pd.get_dummies(df, columns=['sex', 'region']) # n개의 고유값 → n-1열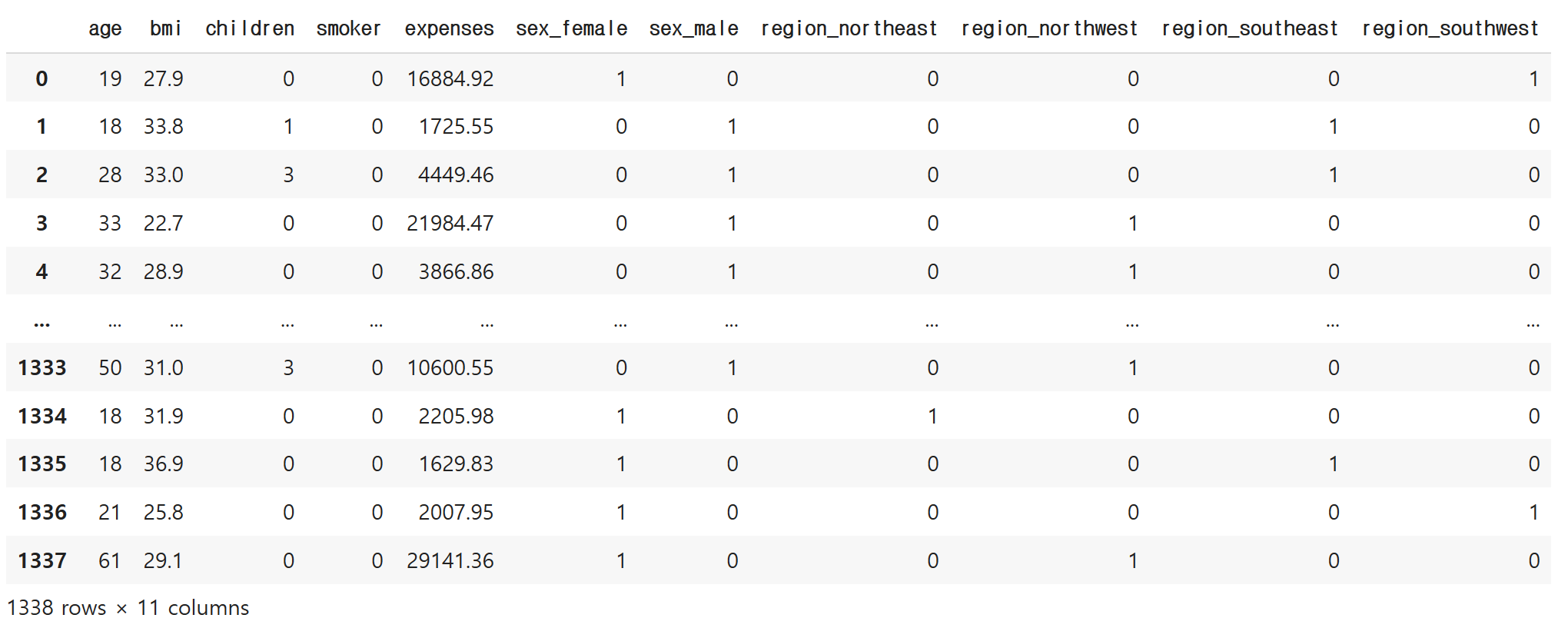
놀랍게도 자동으로 1or0으로 변한 것을 알 수 있습니다.
단, 우리는 열이 많아지면 계산을 많이 해야 합니다.
따라서 열 갯수를 줄여야 합니다.
어떻게?
pd.get_dummies(df, columns=['sex', 'region'], drop_first=True)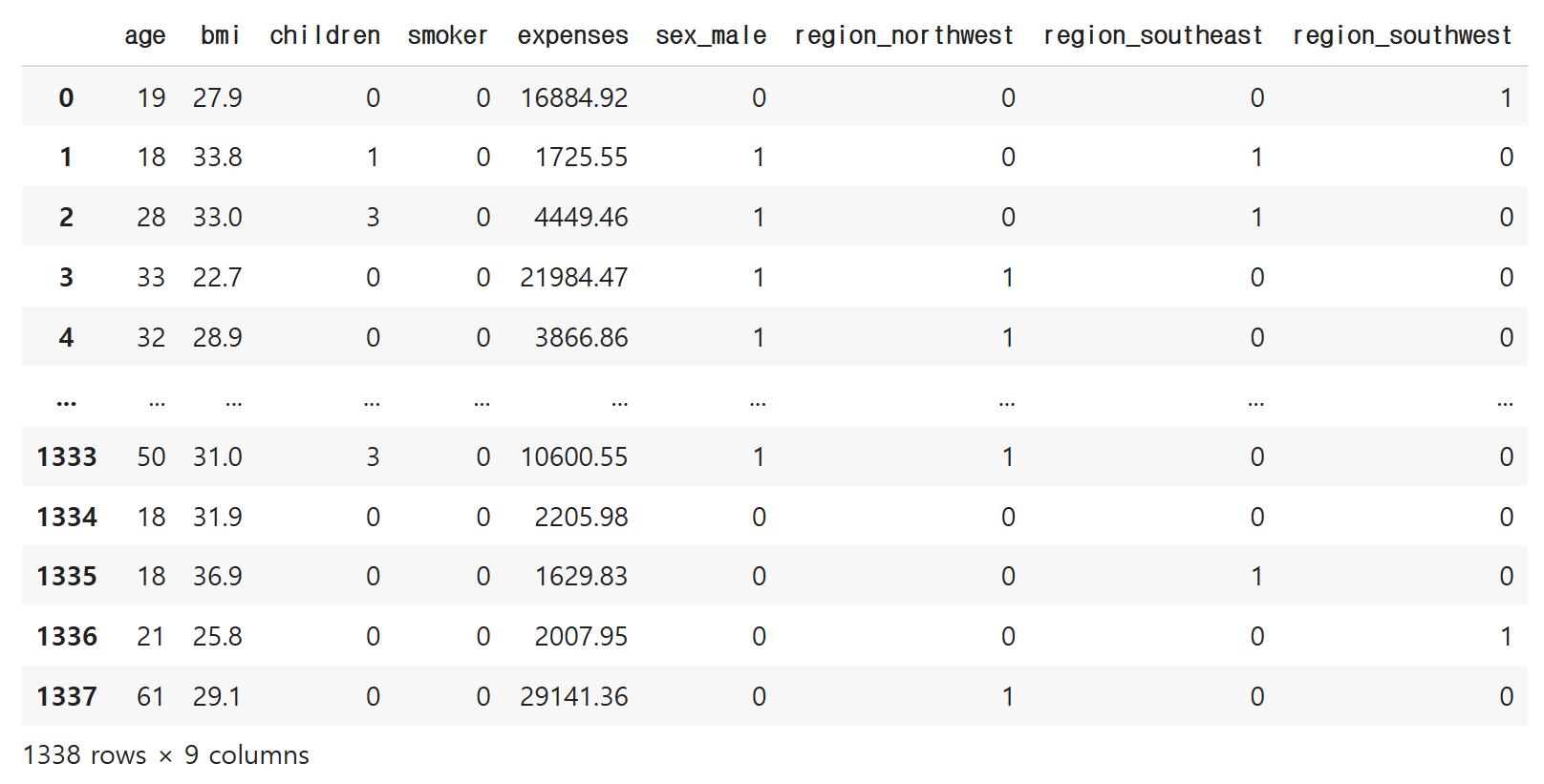
혹시 수 있으니까, df2로 복사해 줍니다.
df2 = df.copy()
df = pd.get_dummies(df, columns=['sex', 'region'], drop_first=True)
df 다시 확인
df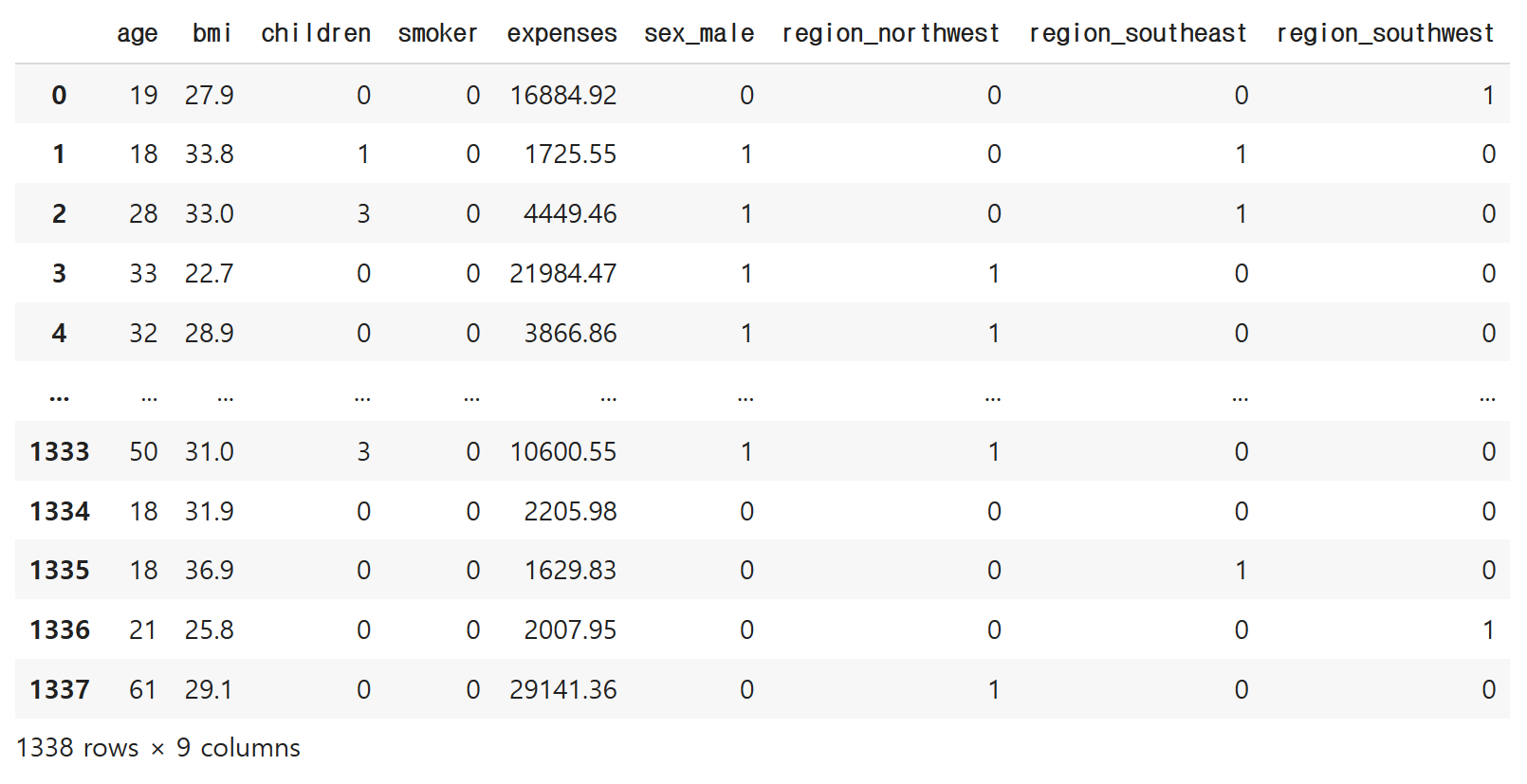
훈련셋과 시험셋 나누기
데이터를 넣어서 모델을 학습시킨 다음에 해당 모델을 가지고 새로운 값을 넣어서
결과를 받아내는 프로그램 입니다.
기존에 학습에 쓰인 데이터가 아니라 새로운 데이터를 넣어서 검증을 해줘야 합니다.
일반적으로 데이터가 100개가 있다면, 70~80개는 학습에 사용,
20~30개는 시험을 위한 데이터셋으로 남겨놓습니다.
(달라질수 있습니다)
모델링이란
모델링은 데이터 분할 작업입니다.
1. 종속변수(소문자 y)와 독립변수(대문자 X)를 분리합니다.
대소문자 구분에 유의하세요
독립변수는 작업을 하면서 종속변수에 영향을 줍니다.
2. 학습셋(=훈련셋)과 시험셋(test set)을 분리합니다.
이는 학습의 결과에 대한 신뢰성, 정확성을 검증합니다.
| 독립변수 | 종속변수 | |
| 학습셋 | X_train | y_train |
| 시험셋 | X_test | y_test |
자 독립변수와 종속변수를 잠깐 보겠습니다.
독립변수는 예측에 사용되는 일종의 재료같은 변수들입니다.
피쳐(feature), 피쳐 변수(feature variable)라고도 합니다.
종속변수는 예측의 대상이 되는 변수입니다.
목표 변수, 타겟 혹은 타겟 변수(target variable)라고도 합니다.
지도 학습에 속하는 모델은 독립변수를 통해 종속변수를 예측합니다.
어떠한 변수가 종속변수인지 정확하게 알려줘야 합니다.
독립변수와 종속변수를 각각 별도의 데이터로 입력받게 됩니다.
- (model.fit(X : 독립변수, y : 종속변수))
df # Y : expenses / X : 독립변수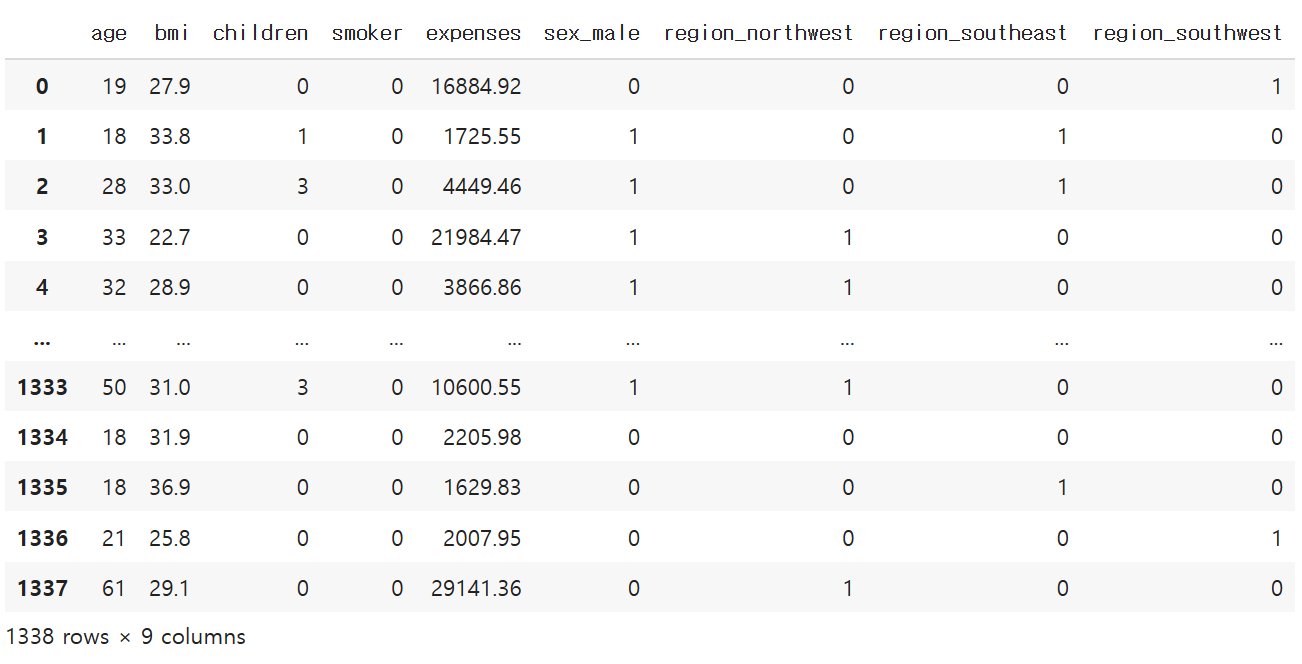
독립변수와 종속변수 확인
X = df.drop('expenses', axis=1) # 독립변수들
y = df['expenses'] # 목표변수/타깃변수/종속변수
X, y( age bmi children smoker sex_male region_northwest \
0 19 27.9 0 0 0 0
1 18 33.8 1 0 1 0
2 28 33.0 3 0 1 0
3 33 22.7 0 0 1 1
4 32 28.9 0 0 1 1
... ... ... ... ... ... ...
1333 50 31.0 3 0 1 1
1334 18 31.9 0 0 0 0
1335 18 36.9 0 0 0 0
1336 21 25.8 0 0 0 0
1337 61 29.1 0 0 0 1
region_southeast region_southwest
0 0 1
1 1 0
2 1 0
3 0 0
4 0 0
... ... ...
1333 0 0
1334 0 0
1335 1 0
1336 0 1
1337 0 0
[1338 rows x 8 columns], 0 16884.92
1 1725.55
2 4449.46
3 21984.47
4 3866.86
...
1333 10600.55
1334 2205.98
1335 1629.83
1336 2007.95
1337 29141.36
Name: expenses, Length: 1338, dtype: float64)
여기서 필요한 작업!
사이킷런(dcikit-learn)을 설치해줍니다.
사이킷런은 파이썬에서 사용하는 머신러닝 용 라이브러리 입니다.
훈련셋과 시험셋을 나누는데 사용합니다.
from sklearn.model_selection import train_test_split # 훈련셋/ 시험셋 나눠주겠다
학습(훈련)셋과 시험셋
🚗학습셋과 시험셋을 구분하지 않고고 예측 모델을 만들면
새로운 데이터에 대한 예측력을 검증할 수 없습니다
(기출문제를 학습시키고 다시 그 문제로 시험을 보는 것이 나을 것)
전체 데이터를 갖고 모델링을 하고, 또다시 전체 데이터에 대해서
예측값을 만들어서 종속변수를 비교합니다.
이것은 특정 데이터에 대해 과최적 되어 있을 수 있습니다.
*과최적 : 모델을 특정 데이터에 대해서 과도화게 최적화 되는 경우
선형에선 의도한 바대로 데이터가 좌상향 직선 모습을 그리지 못하는 경우
변수 잠깐 정리
train_test_split(X: 독립변수들, y:종속변수, test_size=시험셋의 비율, random_state=랜덤값 기준)
test_size : 전체 비율이 1이라고 했을 때, test set의 사이즈 (0.2~0.3)
random_state : numpy.random.seed() → 똑같은 값이 나와줄 수 있도록 기준을 잡아줌
train_test_split(X, y) : 4개
(1. X 훈련셋, 2. X 시험셋, 3. y 훈련셋 4. y 시험셋) test_size 훈련 : 시험의 비율 = 8 : 2
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=15)
다시
# X(독립변수들) 훈련셋
X_train # 1338 * 0.8
# X(독립변수들) 시험셋
X_test # 1338 * 0.2
# y(종속변수) 훈련셋
y_train
# y(독립변수들) 시험셋
y_test38 39774.28
126 17081.08
479 1824.29
10 2721.32
195 1639.56
...
1059 4462.72
303 4349.46
335 13822.80
792 2731.91
1213 10806.84
Name: expenses, Length: 268, dtype: float64
모델 학습
모델링은 머신러닝 알고리즘으로 모델을 학습시키는 과정입니다.
결과물은 머신러닝 모델이죠.
이를 위해선 모델링에 사용할 머신러닝을 선택해야 합니다.
우리는 독립변수와 종속변수를 fit( )함수에 인수로 주어서
학습시키도록 하겠습니다.
| (1) 알고리즘 선택 | (2) 모델 생성 | (3) 모델 학습 | (4) 모델을 사용한 예측 |
| 다양한 머신러닝 알고리즘 중에서 선택후 라이브러리를 import 합니다. | 모델링에 사용할 모델을 생성합니다 |
fit( ) 함수에 학습셋의 독립변수와 종속변수를 인수로 대입합니다. | train_test_split( )의 함수에 시험셋의 독립변수를 인수로 대입합니다. |
이번엔 사이킷런의 선형 모델을 불러옵니다.
from sklearn.linear_model import LinearRegression
모델 정의
model = LinearRegression()
이제 모델 훈련 (모델 학습)도 진행합니다.
model.fit(X_train, y_train)LinearRegression()
.predict()로 예측할 수 있습니다.
pred = model.predict(X_test)
predarray([33898.61270574, 25232.45759924, 3804.50645037, 3228.49104449,
2756.81278809, 8033.21035704, 987.12020052, 35008.26691978,
8457.65258379, 8809.2440256 , 3912.41210232, 6212.41352556,
35992.98987316, 32784.11761539, 5529.03404042, 37345.16203035,
27195.86089827, 9378.13909815, 30163.64645346, 8237.58056189,
5443.54809722, 9758.3695261 , 3383.83412347, 18574.74616843,
11854.24801585, 8693.98633682, 7691.27758526, 39057.47312889,
3700.25074544, -55.32108627, 6892.11946391, 9261.58589699,
5493.91232704, 41131.11464335, 6963.6286208 , 5581.02849751,
5456.31019908, 3826.32007054, 6318.38279297, 11576.5876286 ,
7173.45042344, 10789.68608735, 15750.03337219, 2713.16660825,
11163.18705589, 11255.2186619 , 11667.74048969, 6440.91151386,
# 13줄부터 67줄까지는 지면의 한계상 생략합니다.
새로운 데이터를 넣어서 예측했습니다.
모델 평가
일단은 기초적으로, 테이블로 평가해보겠습니다.
actual 이 실제 값, pred가 예측 값 입니다!
# 테이블로 평가
comparison = pd.DataFrame({
'actual': y_test, # 실제값
'pred': pred
})
comparison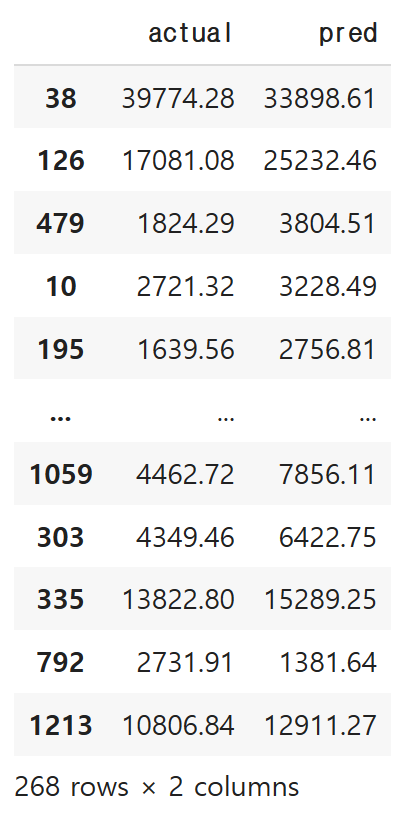
🤔예측이 잘 되었을까요?
seaborn과 matplotlib.pyplo을 사용하여 스캐터그래프를 그려봅시다.
import seaborn as sns
import matplotlib.pyplot as plt
라이브러리를 임포트 했습니다.
plt.figure(figsize=(17,10))
sns.scatterplot(x = 'actual', y = 'pred', data = comparison)
plt.title("Linear_regression_model")
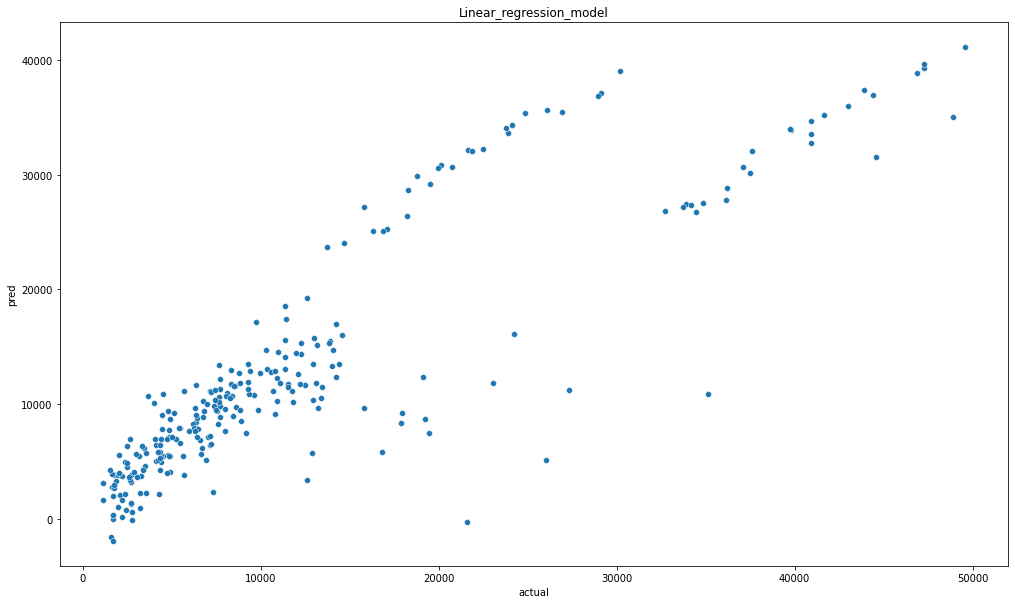
정확한 선형은 아니지만 진행이 된것 같네요.
선형을 그릴 수 있는 그래프로 나타내보겠습니다.
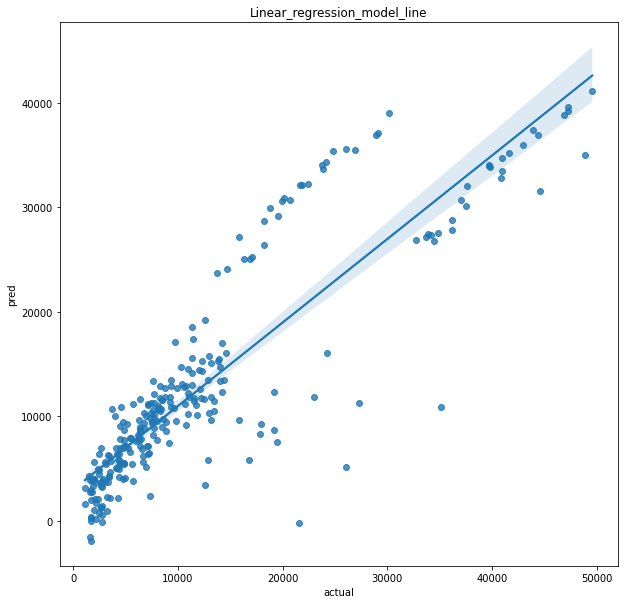
🤗
좋습니다.
이제부터는 회귀분석에서 기계학습의 목표(최소화해야 하는)가 될 오차들을 알아보겠습니다.
RMSE & R²(결정계수)
회귀는 연속형 변수를 예측할 때 쓰입니다.
이 오차들을 기준으로 모델의 성능이 결정됩니다.
이를 평가하기 위해 쓰이는 것들이 MSE, RMSE, R² 입니다
| 평가지표 | 설명 |
| MAE(Mean Absolute Error, 평균 절대 오차) | 실제값과 예측값 사이의 오차에 절댓값을 씌운 뒤 이에 대한 평균을 계산 |
| MSE(Mean Squared Error, 평균 제곱 오차) | 실제값과 예측값 사이의 오차를 제곱한 뒤 이에 대한 평균을 계산 |
| RMSE(Root Mean Absolute Error, 루트 평균 제곱 오차) | MSE에 루트를 씌운 값 연속형 변수를 예측할 때 가장 일반적으로 사용 되는 평가 지표 |
| R² | 결정계수 독립변수가 종속변수를 얼마만큼 설명해주는지 나타내는 지표, 즉 설명력 |
MAE, MSE, RMSE의 공통점은 모두 0에 가까울 수록 좋다는 점입니다.
단 R²는 1에 가까울 수록 좋습니다.
사이킷런에서 한번 알아보겠습니다.
mean_squared_error()
임포트 진행
from sklearn.metrics import mean_squared_error
MSE는 mean_squared_error로 계산합니다.
실제값과 예측값 사이의 오차를 제곱한 후 ,이의 평균을 계산한 것이죠.
아래에서 볼까요?
mse1 = mean_squared_error(y_test, pred)
mse1
# 모델 간 비교 ( 다른 알고리즘, 다른 독립변수 조합)29847759.53792107
RMSE는 두가지 방식이 있습니다.
먼저, **0.5를 걸어서 루트를 씌우는 방식이 있습니다.
rmse1 = mean_squared_error(y_test, pred) ** 0.5
rmse15463.310309502936
두번째로, squared 속성에 False를 걸어 루트값을 나타내는 방식이 있습니다.
rmse2 = mean_squared_error(y_test, pred, squared=False)
rmse25463.310309502936
둘다 값은 똑같습니다만, 안정적인 것은 두번째입니다.
두번째를 활용하도록 하겠습니다.
R²는 model.score( ) 에 학습시킨 독립변수와 종속변수를 넣으면 됩니다.
model.score(X_train, y_train) # R²0.7455515454595125
이렇게 구성됬습니다.
어떤가요? 1과 가까워졌나요?
이번 보험료 선형회귀 분석은 지면이 상당히 길어지는 관계로
여기서 마치고, 다음 시간부터는 R²에 대한 공식 설명부터 진행하도록 하겠습니다.
직접 실습이 실력을 향상하는 가장 좋은 방법입니다.
'머신러닝 > 지도학습' 카테고리의 다른 글
| [Machine Learning] 결정트리_회귀(Regression) 실습 사례- 보험비 (0) | 2022.12.22 |
|---|---|
| [Machine Learning] 결정트리 알고리즘 분류 실습사례_wine (0) | 2022.12.22 |
| [Machine Learning] KNN 알고리즘 실습사례_wine 분류2_solution (0) | 2022.12.21 |
| [Machine Learning] KNN 알고리즘 실습사례_wine 분류 (0) | 2022.12.19 |
| 선형회귀 ep2. 결정계수에 관하여 (2) | 2022.12.16 |



