본 문서는 GPU-Net과 블랙박스 최적화 기법에 대한 설명 중 LA-MCTS에 대한 설명은 찾기 어려워
직접 정리하고자 한 게시글 입니다.
개념에 대해서 길게 설명한 글도 존재하지만, 수학적인 베이스가 상당히 많이 필요한 관계로
sin 그래프를 사용한 예시를 보며 간단하게 설명해보겠습니다.
먼저, 기본적으로 LA-MCTS는 지연 행동을 활용한 몬테 카를로-트리 검색기법 입니다.
몬테 카를로-트리 검색은 이미 국내에 소개된 바 있습니다.
몬테카를로 트리 탐색 - 위키백과, 우리 모두의 백과사전 (wikipedia.org)
몬테카를로 트리 탐색 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 컴퓨터 과학에서 몬테카를로 트리 탐색(Monte Carlo tree search, MCTS)은 모종의 의사 결정을 위한 체험적 탐색 알고리즘으로, 특히 게임을 할 때에 주로 적용된다. 선
ko.wikipedia.org
일종의 포커나 체스 등과 같은 게임에서 승리를 위해 최적화 하는 것을 생각해 주시면 좋을것 같습니다.
LA-MCTS는 이와 유사하게 1) 학습과 분할 2) 선택 3) BO, 서포트 벡터 머신 등을 활용한 샘플링으로 나눠집니다.
재귀적인 파티셔닝을 통해 가능성 높은 영역을 찾습니다. 이때 차용하는 것이 latent action입니다.

* 보이지 않는 공간에 규제 영역을 만들고, 이 규제에 따라서 행동하도록 만드는 것입니다.
잠재 공간이라고 부를 수 있겠습니다.
이제 임의의 사인 함수 a를 가정해보겠습니다
참고로 함수 값은 아래와 같습니다.
x = np.arange(0, 10, 0.1)
y = np.sin(2*x)

보시는 바와 같이 a에서 b와 c가 분리되서 c가 떨어져나가고,
d와 e가 분리되서 e가 떨어져나가고, f에서 h와 i가 분리되고 ... 이런 식으로 실패에 대해 loss를 반복하는 것입니다.
이를 그래프 상으로 옮겨 보겠습니다.

c는 버리는 영역이 됩니다.

아랫단으로 진행하고, e는 버리는 영역이 됩니다.

g영역이 버리는 영역이 됩니다.
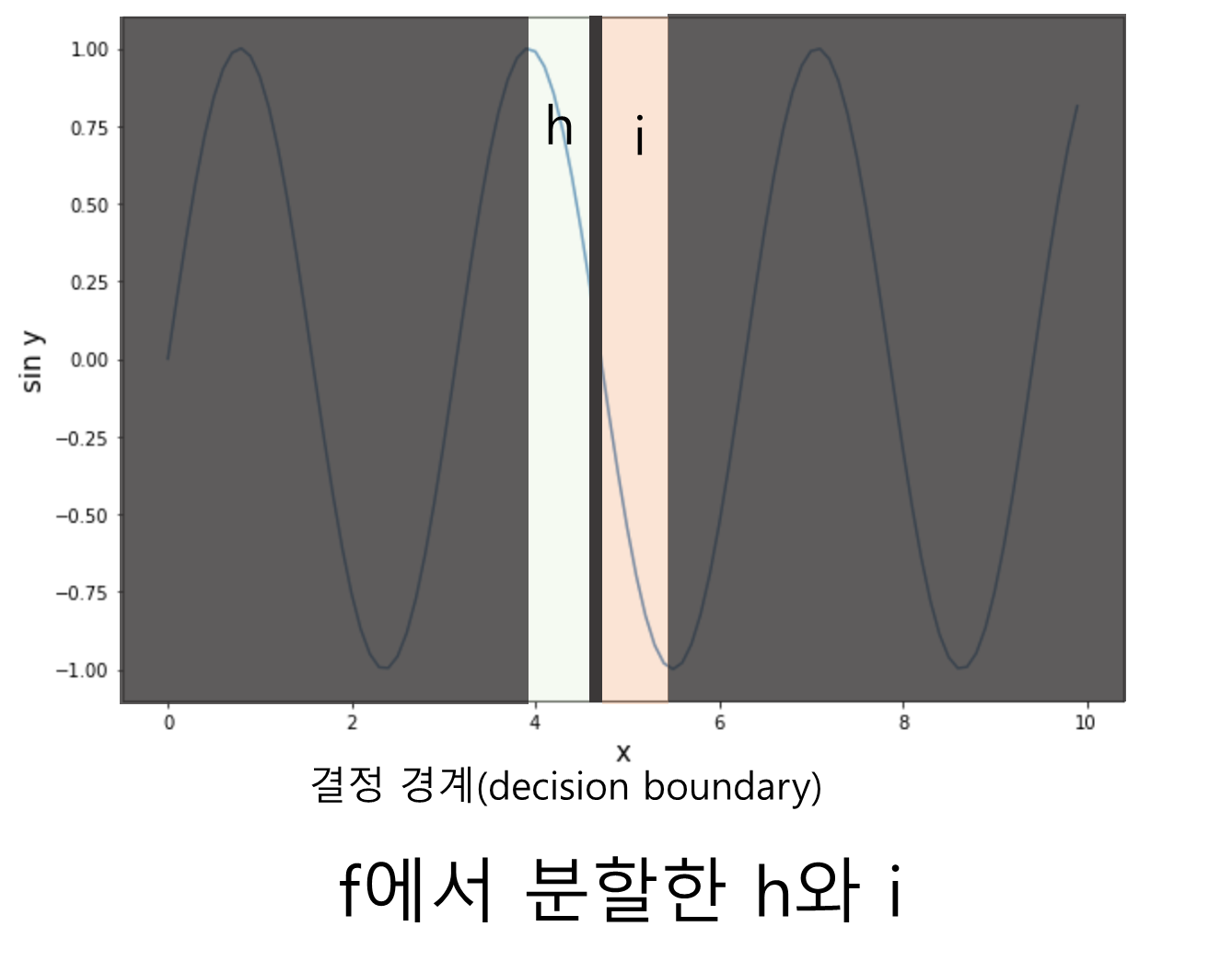
결과적으로 h가 남게되는데요.
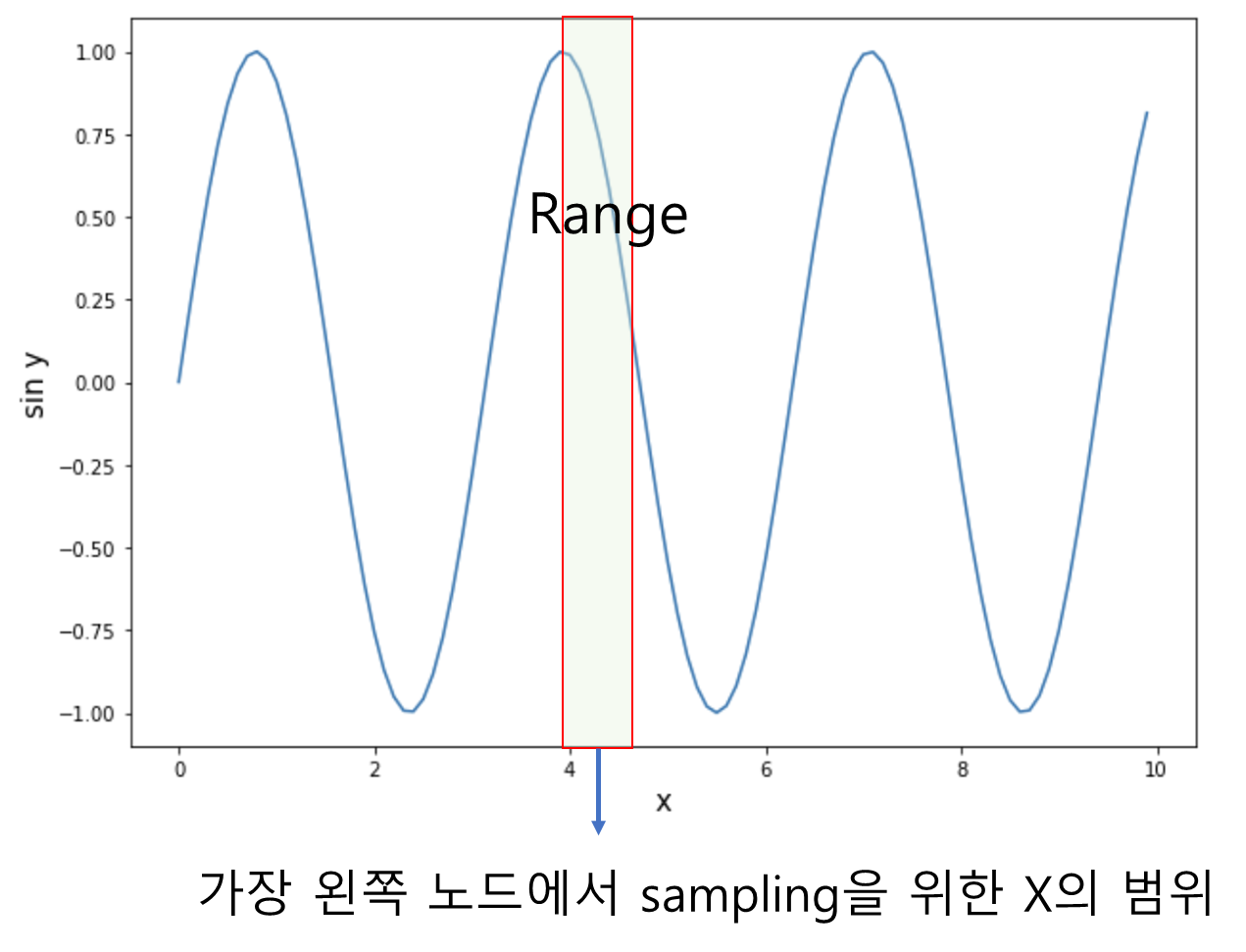
이 과정이 LA-MCTS를 사용한 sin(x)를 1차원으로 분할하는 시각화 내용이었습니다.
개발진들은 어떤 노드든지 샘플 사이즈가 분할 한계점(threshold) θ를 넘어가는 한 잠재 공간 행동을 사용해서 재귀적으로 노드를 분할합니다.
요컨대 분할 표준을 만족할 노드가 더 없을 때까지 트리를 분할합니다.
그러면, 이 트리는 아래 네 단계의 반복을 진행할 준비가 된 것입니다.
UCB 알고리즘을 사용하는 선택
- Upper Confidence Bound
SanghyukChun's blog 참조
Machine learning 스터디 (20-1) Multi-armed Bandit - README (sanghyukchun.github.io)
Machine learning 스터디 (20-1) Multi-armed Bandit - README
들어가며 이 글에서는 reinforcement learning의 한 갈래 중 하나인 Multi-armed Bandit에 대해 다룰 것이다. Multi-armed Bandit이 어떤 문제인지에 대해 간략히 설명한 다음, 좀 더 formal하게 문제를 정의하고, 이
sanghyukchun.github.io
BO(베이지안 최적화)를 사용하는 샘플링
- Bayesian Optimizations
TuRBO를 사용하는 샘플링
- TuRBO는 Trust region Bayesian Optimizations를 의미합니다.
- 베이지안 최적화의 다른 버전입니다.
표준 BO를 사용하는 샘플링
결과적으로는 사용자는 acquisition 함수로부터 가장 큰 값을 계산할 수 있는 샘플을 찾을 수 있게 됩니다.
'딥러닝 > 신규 모델&기술 설명' 카테고리의 다른 글
| [논문 리뷰] GAN에서 한 발짝 앞서서, PGAN(Progressive-GAN) 기술 분석 (2) | 2023.03.11 |
|---|---|
| [Deep Learning] YOLOP v2 / 더 향상된 욜로 모델! - 논문리뷰 (0) | 2023.03.01 |
| [DeepLearning] YOLOv 모델, you only look once 논문 분석 (0) | 2023.02.27 |
| [DeepLearning] IRB에 관하여 (0) | 2023.02.15 |
| [DeepLearning] GPU-Net을 활용한 이미지 분류_1 (0) | 2023.02.13 |



