
서론
지난 시간에 이어서, 서울시 농수축산물 가격 데이터에 대해서 분석을 진행합니다.
몇가지 수정되야 할 점이 있어서 , 따로 정리했습니다.
1) 2021년 한 해의 데이터만으로는 변화하는 양상을 보기 어려울 것으로 판단,
2019년과 2020년의 데이터를 조회하여 3년간의 양상을 살펴봅니다.
2) 날짜 데이터인 년도-월에 대해서 월을 빼고 , 연도만 조회해서 사용합니다.
3) 이 날짜 데이터도 독립변수에 포함하게 됩니다.
4) DecisionTree 회귀 모델을 통해서 score를 높이게 됩니다.
시작
df_19 = pd.read_csv('생필품 농수축산물 가격 정보(2019년).csv', encoding = 'cp949')df_20 = pd.read_csv('생필품 농수축산물 가격 정보(2020년).csv', encoding = 'cp949')df_21 = pd.read_csv('생필품_농수축산물_가격_정보(2021년).csv', encoding = 'cp949')
2019년~2021년 데이터를 df_19, df_20, df_21로 로드하여, 모두 품목을 합하여 사용하려 합니다.
merge 함수를 이용합니다.
이경우 merge를 통해서 2019년과 2020년의 데이터를 합하고, 이를 2021년과 합하여
중복되는 공통된 품목번호, 시장마트번호 등을 남길 것입니다.
다행이 3년간 동일한 품목 번호를 유지하고 있습니다.
df_one = pd.merge(df_19, df_20, how = 'outer')df_two = pd.merge(df_one, df_21, how = 'outer')df = df_two
df
불필요한 열 모두 삭제합니다.
# 아래부터 필요없는 행 제거 예정
# 주의
df.drop(['시장유형 구분(시장/마트) 이름','시장유형 구분(시장/마트) 코드'], axis = 1, inplace = True)df.drop(['자치구 이름','시장/마트 이름'],axis=1, inplace = True)df.drop(['점검일자','실판매규격','품목 이름','비고','일련번호'], axis = 1, inplace = True)
df # drop된 내용 확인
# 가격이 0원인 상품, 1원인 상품 iloc로 삭제
df = df.iloc[3695:,:]
df
# 23억, 3500만원, 3490만원어치 상품 삭제 (outlier)
df = df.iloc[:317145]
df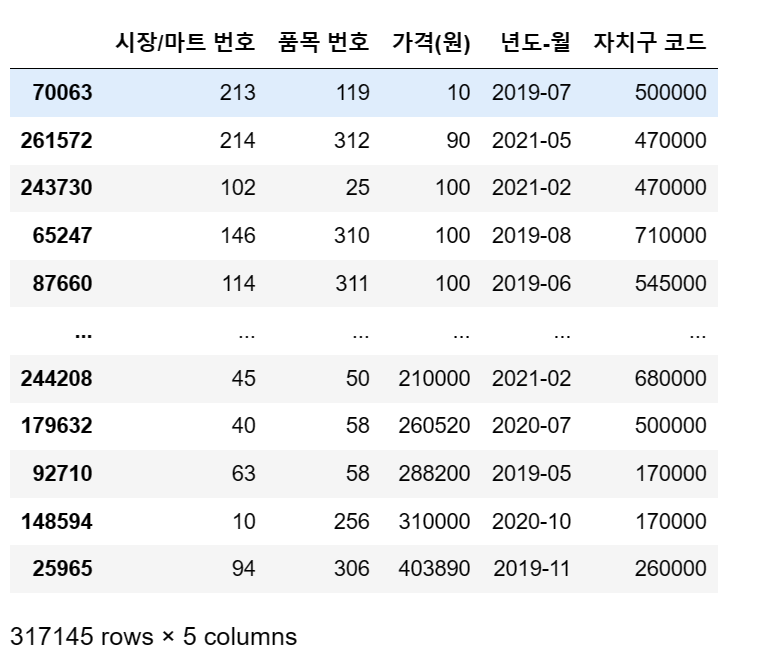
연도별로 전부 날짜를 전환합니다.
이 작업으로 3년간 물가폭이 증가하는지, 하락하는지 확인할 수 있습니다.
# 년도-월을 전부 연도별로 바꾸기
df['년도-월'] = pd.to_datetime(df['년도-월'])
df['년도-월'] = df['년도-월'].dt.yeardf
결측치는 없어집니다.
df.isnull().sum() # 결측치 확인시장/마트 번호 0
품목 번호 0
가격(원) 0
년도-월 0
자치구 코드 0
dtype: int64
지난시간에 중복했던 코드들을 모두 제외하면
아래의 데이터프레임이 결과적으로 남게 됩니다.
종속변수와 독립변수는 모두 포함되어 있습니다.

다시 정리하자면, 독립변수 X는 아래와 같습니다.
시장/마트 번호, 품목 번호, 년도-월, 자치구코드
종속변수 y는 아래와 같습니다.
가격(원)
시각화를 진행해봅니다.
자치구별로 몇가지 가격이 다른점이 보입니다.
# 자치구 - 가격별로 시각화
plt.figure(figsize = (13,9))
sns.lineplot(data = df.head(10000), x='자치구 이름', y = '가격(원)')
plt.show()
강남구가 상당히 높은 곳이 있는 곳으로 확인됩니다.
서대문구와 서초구도 보이네요.
다음엔 가장 가격대가 높았던 10가지 정도 품목을 찾아왔습니다.
# 품목 - 가격별로 시각화
plt.figure(figsize = (13,4))
sns.barplot(data = df.tail(10), x='품목 이름', y = '가격(원)')
plt.show()
꽤 높은등급의 배가 많았을까요? 신고배와 한우 쇠고기가 위치하고 있습니다.
각 마트+시장별로 전체 가격이 높은 곳을 10곳만 찾아보았습니다.

전통시장과 대형마트, 둘중 어떤 곳이 가격이 더 높았을까요?

자치구 별로 시장+마트가 많은 곳은 어떤 곳이었을까요?
# 자치구 - 시장/마트 갯수
plt.figure(figsize = (13,9))
sns.barplot(data = df.tail(100), x = '자치구 이름', y = '시장/마트 번호', palette='rainbow')
plt.show()
전통시장과 대형마트 중 어떤 곳이 더 가격이 높은 폭으로 상승했을까요?
# 연도 - 가격- 시장/마트 유형 구분별로 시각화
plt.figure(figsize = (13,9))
sns.lineplot(data = df, x='년도-월', y = '가격(원)', hue = '시장유형 구분(시장/마트) 이름')
plt.show()
# 연도별로 가격이 구분되는 추이(시장 vs 대형마트)
이제 불필요한 행은 모두 제거하겠습니다.
# 아래부터 필요없는 행 제거 예정
# 주의
df.drop(['시장유형 구분(시장/마트) 이름','시장유형 구분(시장/마트) 코드'], axis = 1, inplace = True)df.drop(['시장/마트 이름'],axis=1, inplace = True)df.drop(['점검일자','실판매규격','품목 이름','비고','일련번호'], axis = 1, inplace = True)
훈련셋/ 검증셋 구분합니다
# X,y 를 다르게 구분해서 훈련 시작
X = df.drop('가격(원)', axis = 1)
y = df['가격(원)']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 10)
이제 지난시간에 한계점을 보였던 선형회귀를 돌파해봅시다!
다시 모델을 선언합니다.
model = LinearRegression()
model.fit(X_train, y_train)LinearRegression()
예측값 확인합니다.
pred = model.predict(X_test)
predarray([6881.99779365, 4844.49591765, 3705.79777136, ..., 3982.46544955,
4584.29962765, 3629.85783588])
MSE, RMSE, 결정계수들도 볼까요?
mean_squared_error(y_test, pred)
# MSE52885519.83597086
RMSE
# rmse
mean_squared_error(y_test, pred) ** 0.57272.243108970633
R² 여전히 높게 뛰진 않았습니다.
model.score(X_train, y_train) # R²0.0727616965554323
시각화로 진행해봅니다.
comparison = pd.DataFrame({
'actual': y_test, # 실제값
'pred': pred
})
comparison
실제값과 예측값을 갖고 선형으로 그려봅니다.
plt.figure(figsize=(20, 12))
sns.regplot(x = 'actual', y= 'pred', data = comparison)
plt.show()
이제 결정트리 DecisionTree의 회귀 모델로 진행해봅니다!
최대 깊이를 높여서 예측 정확도를 높이려고 합니다.
# 모델 설정
model = DecisionTreeRegressor(random_state=10, max_depth = 500)model.fit(X_train, y_train)
pred = model.predict(X_test)
예측값 반환합니다.
predarray([7429.13043478, 5415.09433962, 3396.48148148, ..., 5769.81132075,
4585. , 2287.54716981])
이번에도 MSE, RMSE, MAE를 평가해봅니다.
# mse 평가
mean_squared_error(y_test, pred)4745971.50434268
# rmse 평가
mean_squared_error(y_test, pred, squared=False)2178.5250754450085
# mae 평가
mean_absolute_error(y_test, pred)910.0346657466318결정계수 입니다.
model.score(X_train, y_train) # R²
# 0.89점0.8906056519778784
결정트리의 나무도 진행해봤습니다.
plt.figure(figsize=(20, 10)) # 그래프 크기 설정
plot_tree(model, max_depth=10, fontsize=20)
plt.show() # 로딩시간 다수에 주의 (10분)
최소자승법을 이용해 오차를 최소화하려 노력하는 Ridge 회귀모델을
시도해 보겠습니다. 필자의 글에서는 아직 시도해보지 않은 모델입니다.
# Ridge회귀 시작
# rmse 구함
ridge = Ridge(alpha = 10)
평균 RMSE 값입니다.
rmse_scores = np.sqrt(-1*neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
avg_rmse6048.972270778937
함수를 통해, alpha(람다.패널티) 값에 따라서 rmse가 어떻게 변화하는지 보겠습니다.
▼ alpha에 대한 개념 참조
https://velog.io/@dlskawns/Linear-Regression-Ridge-Regression-RidgeCV-%EC%A0%95%EB%A6%AC
Linear Regression - Ridge Regression, RidgeCV 정리
오늘 배운 Ridge Regression 및 다항회귀에 대한 정리를 해본다.Rigdge 회귀는 기존 Linear Rigression의 과적합을 해결해주는 굉장히 현실적인 선형회귀방법이다. 너무나 많은 학습으로 인해 과적합되는
velog.io
쉽게, 회귀계수를 조정할 수 있어 객관화를 높일 수 있는 계수입니다.
alphas = [1, 10, 50, 100]
for alpha in alphas :
ridge = Ridge(alpha = alpha)
neg_mse_scores = cross_val_score(ridge, X, y, scoring='neg_mean_squared_error', cv = 9)
avg_rmse = np.mean(np.sqrt(-1*neg_mse_scores))
print('alpha {0}일때 9fold의 평균 rmse: {1:.3f}'.format(alpha, avg_rmse))alpha 1일때 9fold의 평균 rmse: 6048.973
alpha 10일때 9fold의 평균 rmse: 6048.972
alpha 50일때 9fold의 평균 rmse: 6048.968
alpha 100일때 9fold의 평균 rmse: 6048.962
각 alpha별 회귀계수를 데이터프레임으로 표현합니다.
이를 갖고 barplot으로 시각화합니다.
# alpha (0~100)에 따른 피처별 회귀 계수를 데이터프레임으로 표시
fig, axs = plt.subplots(figsize=(18,10), nrows=1, ncols=4)
coeff_df = pd.DataFrame()
for pos, alpha in enumerate(alphas):
ridge = Ridge(alpha = alpha)
ridge.fit(X, y)
coeff = pd.Series(data=ridge.coef_, index = X.columns)
colname = 'alpha:'+str(alpha)
coeff_df[colname]=coeff
coeff = coeff.sort_values(ascending =False)
axs[pos].set_title(colname)
axs[pos].set_xlim(-3, 6)
sns.barplot(x=coeff.values, y=coeff.index, ax=axs[pos], palette = 'icefire')
plt.show()
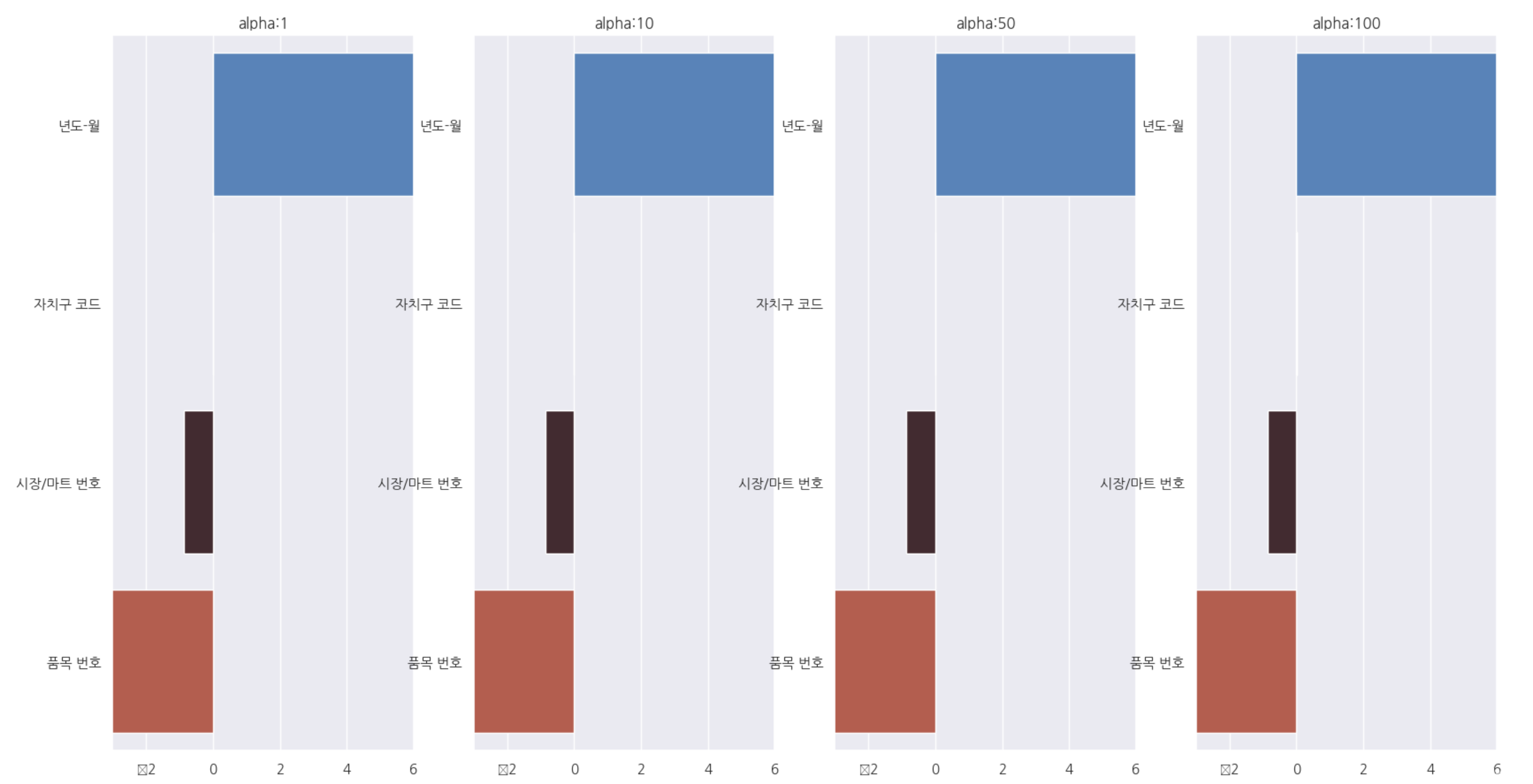
릿지의 점수도 볼까요?
ridge.score(X_train, y_train)0.07275983743143855
회귀모델에 LightGBM을 적용한 모델링도 확인해봅니다.
랜덤서치CV를 사용해보았습니다.
#LightGBM 시도
# # 사용할 params정의
params = {"n_estimators" : [100, 500, 1000],"learning_rate" : [0.01, 0.05, 0.1, 0.3]
,"lambda_l1" : [0, 10, 20],"lambda_l2" : [0, 10, 20],"max_depth" : [5, 10, 15, 20],"subsample": [0.6, 0.8, 1]}model = LGBMRegressor(random_state = 100)
new_model = RandomizedSearchCV(model,
param_distributions = params,
cv = 9,
random_state=100, n_jobs = -1)new_model.fit(X_train, y_train) # 시간 소요 체크RandomizedSearchCV(cv=9, estimator=LGBMRegressor(random_state=100), n_jobs=-1,
param_distributions={'lambda_l1': [0, 10, 20],
'lambda_l2': [0, 10, 20],
'learning_rate': [0.01, 0.05, 0.1, 0.3],
'max_depth': [5, 10, 15, 20],
'n_estimators': [100, 500, 1000],
'subsample': [0.6, 0.8, 1]},
random_state=100)
베스트 점수를 구현해봅니다.
new_model.best_score_ # 최적의 점수계산0.8681272044157713
최적의 패러미터 구현합니다.
new_model.best_params_{'subsample': 0.8,
'n_estimators': 1000,
'max_depth': 5,
'learning_rate': 0.1,
'lambda_l2': 0,
'lambda_l1': 0}
mse 평가
# mse 평가
mean_squared_error(y_test, pred)5755554.830311395
rmse 평가
# rmse 평가
mean_squared_error(y_test, pred, squared=False)2399.0737442420136
결정계수 구현
new_model.score(X_train, y_train)0.8730338231771096
# 테이블로 평가
comparison = pd.DataFrame({
'actual': y_test, # 실제값
'pred': pred
})
선형모델과 같이, regplot으로 표현합니다.
# regplot 제작
plt.figure(figsize=(10, 7))
sns.regplot(x = 'actual', y= 'pred', data = comparison)
plt.show()
마지막으로, KFold 기법을 사용한 randomforest 회귀모델을
적용해보겠습니다.
# 랜덤 포레스트 시작 + Kfold 5개
from sklearn.model_selection import KFold
from sklearn import ensemble
kf = KFold(n_splits = 5)
split한 독립변수 데이터입니다.
list(kf.split(X))[(array([ 63429, 63430, 63431, ..., 317142, 317143, 317144]),
array([ 0, 1, 2, ..., 63426, 63427, 63428])),
(array([ 0, 1, 2, ..., 317142, 317143, 317144]),
array([ 63429, 63430, 63431, ..., 126855, 126856, 126857])),
(array([ 0, 1, 2, ..., 317142, 317143, 317144]),
array([126858, 126859, 126860, ..., 190284, 190285, 190286])),
(array([ 0, 1, 2, ..., 317142, 317143, 317144]),
array([190287, 190288, 190289, ..., 253713, 253714, 253715])),
(array([ 0, 1, 2, ..., 253713, 253714, 253715]),
array([253716, 253717, 253718, ..., 317142, 317143, 317144]))]
함수를 이용할 예정인데요? 모델별로 트리의 갯수를 높여가며, mse와 rmse점수를
리스트에 써서 구해봅니다.
list1 = []
list2 = []
nTreeList = range(1, 100, 10)
for i in nTreeList:
depth = None
maxFeat = 4
model = ensemble.RandomForestRegressor(n_estimators=i,
max_depth=depth, max_features=maxFeat,
oob_score=False, random_state=11)
model.fit(X_train, y_train)
pred = model.predict(X_test)
list1.append(mean_squared_error(y_test, pred))
list2.append(mean_squared_error(y_test, pred, squared = False))
print("MSE")
print(list1)
print('RMSE')
print(list2)MSE
[5334428.690946911, 4800656.80543549, 4838638.738920654, 4818637.282341971, 4815386.480296213, 4804108.810000638, 4793764.238040956, 4777475.016744278, 4774681.616097125, 4775541.113167785]
RMSE
[2309.6382164631136, 2191.0401195403724, 2199.6906007256234, 2195.139467628873, 2194.3988881459572, 2191.827732738282, 2189.466656069682, 2185.743584399661, 2185.1044863111524, 2185.3011493082104]
결정계수 확인해봅시다.
model.score(X_train, y_train)0.8904342504659382
현재까지 높은편입니다.
아까 진행했던 n_estimators가 증가하며 rmse가 변하는 추이를 계산해서,
그래프를 그려보겠습니다.
plt.plot(nTreeList, list2)
plt.xlabel('Number of Trees in Ensemble')
plt.ylabel('Root Mean Squared Error')
plt.xlim(0, 18, 2)
plt.ylim(2000, 2500, 100)
plt.show()
tree의 수가 11개정도 되는 지점에서 RMSE는 최솟값을 보이게 됩니다.
이정도의 트리가 가장 적정값인 것이죠.
이렇게하여, 서울시 농수축산물 가격에 대한 회귀모델 분석을 마칩니다.
'머신러닝 > 지도학습' 카테고리의 다른 글
| [Machine learning 평가] Pipeline 형태, Classifier의 평가지표{confusion matrix, 혼동오류, f1 score 개념} (0) | 2023.02.10 |
|---|---|
| [Feature engineering] 데이터 처리 사례_2021 서울시 농산물 가격 분석_1 (0) | 2023.01.01 |
| [Machine Learning] Kaggle_데이터셋 분석_미 초소형 기업 밀도 예측_ep.2 (0) | 2022.12.31 |
| [Machine Learning] Kaggle_데이터셋 분석_미 초소형 기업 밀도 예측 (0) | 2022.12.30 |
| [Machine Learning] Kaggle_데이터셋 분석_Video_Games_Sales.1 (0) | 2022.12.29 |



